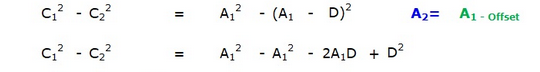This is copy of the livescript i have programmed in Matlab. It is not just a complete algorithm in one equation ,
but a step by step approach so everyone could understand and use this method for custom situations.
I have tested the script with my own channelmaster 1.2m offset dish with a 18 Inch actuator.
I have also programmed an animated plot so also the moves off the actuator and dish are visualised.
I will publish it here when i have converted it to an image that can published at this blog.

Matlab livescript
----------------------------------------------------------------------------------------------
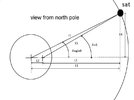
Defining the dish variables
Radius = 370;
The radius between dish pivot and the actuator pivot point on the dish lever (mm)
DishpivotOffset = 190;
The length between dish pivot and the pivot of the actuator mount. (mm)
ActuatorOffset = 48;
Length between actuator pivot point and the centre of the actuator mount. (mm)
MinActuatorLength = 210;
MaxActuatorLength = 550;
Minimal en maximum actuator extensions. (mm)
ActPivToRadiusMin = sqrt( ( (ActuatorOffset^2) + (MinActuatorLength^2) ) ) ;
ActPivToRadiusMax = sqrt( ( (ActuatorOffset^2) + (MaxActuatorLength^2) ) ) ;
Calculate the distances between the actuator pivot and the actuator pivot on the
disk lever for the minimal and maximum actuator lengt. (Pythagorean theorem)
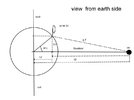
Pact = [ 0 ; 0 ];
Pdsh = [ 0 ; DishpivotOffset ];
Ract = ActPivToRadiusMin ;
Rdsh = Radius ;
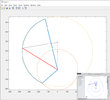
Definition off the coordinates for both virtual circles of the actuator and the dish.
This the definition of the virtual circles for minimal extended actuator.
Given is a virtual circle with a center point M (a, b) and a radius r.
So for every point on the virtual circle i have used midpoint equations :
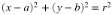
D2 = sum((Pact-Pdsh).^2);
P0 = (Pdsh+Pact)/2+(Rdsh^2-Ract^2)/D2/2*(Pact-Pdsh);
t = ((Rdsh+Ract)^2-D2)*(D2-(Ract-Rdsh)^2);
if t <= 0
fprintf('The circles don''t intersect : initial values not correct.\n')
else
T = sqrt(t)/D2/2*[0 -1;1 0]*(Pact-Pdsh);
Pa = P0 + T;
Pb = P0 - T;
end
The virtual circles are defined as a collecting of points based on a rotating triangle.
I have used the pivot of the actuator as coordinate [ 0 , 0]
Pa and Pb are circles' intersection points . We only need the value Pb.
Pa is the other intersection point which as not important for our calculation.
Pa = Coordinate of the minimal extended actuator .
Pact = [ 0 ; 0 ];
Pdsh = [ 0 ; DishpivotOffset ];
Ract = MaxActuatorLength ;
Rdsh = Radius ;
Definition off the coordinates for both virtual circles of the actuator and the dish.
This the definition of the virtual circles for minimal extended actuator
D2 = sum((Pact-Pdsh).^2);
P0 = (Pdsh+Pact)/2+(Rdsh^2-Ract^2)/D2/2*(Pact-Pdsh);
t = ((Rdsh+Ract)^2-D2)*(D2-(Ract-Rdsh)^2);
if t <= 0
fprintf('The circles don''t intersect : initial values not correct.\n')
else
T = sqrt(t)/D2/2*[0 -1;1 0]*(Pact-Pdsh);
Pc = P0 + T;
Pd = P0 - T;
end
Pc and Pd are circles' intersection points . We only need the value Pd.
Pc is the other intersection point which as not important for our calculation.
Pc = Coordinate of the maximal extended actuator .
Angle = sin (Pb(2) / (DishpivotOffset - Pb(1) ) ) ;
MinAngledegree = Angle / (pi/180);
EastlimitAngle = 90 + MinAngledegree
EastlimitAngle = 67.2740
Angle = sin (Pd(2) / (DishpivotOffset - Pd(1) ) ) ;
MaxAngledegree = (Angle / (pi/180) );
WestlimitAngle = ( 90 + MaxAngledegree ) - EastlimitAngle
WestlimitAngle = 80.0125
Please post reactions or comment .
If someone wanted the Matlab file send me a personal message.
It also possible to copy / paste this script (only remove the
results)